고정 헤더 영역
상세 컨텐츠
본문
https://www.acmicpc.net/problem/1890
1890번: 점프
첫째 줄에 게임 판의 크기 N (4 ≤ N ≤ 100)이 주어진다. 그 다음 N개 줄에는 각 칸에 적혀져 있는 수가 N개씩 주어진다. 칸에 적혀있는 수는 0보다 크거나 같고, 9보다 작거나 같은 정수이며, 가장
www.acmicpc.net
문제
N×N 게임판에 수가 적혀 있다. 이 게임의 목표는 가장 왼쪽 위 칸에서 가장 오른쪽 아래 칸으로 규칙에 맞게 점프를 해서 가는 것이다.
각 칸에 적혀있는 수는 현재 칸에서 갈 수 있는 거리를 의미한다. 반드시 오른쪽이나 아래쪽으로만 이동해야 한다. 0은 더 이상 진행을 막는 종착점이며, 항상 현재 칸에 적혀있는 수만큼 오른쪽이나 아래로 가야 한다. 한 번 점프를 할 때, 방향을 바꾸면 안 된다. 즉, 한 칸에서 오른쪽으로 점프를 하거나, 아래로 점프를 하는 두 경우만 존재한다.
가장 왼쪽 위 칸에서 가장 오른쪽 아래 칸으로 규칙에 맞게 이동할 수 있는 경로의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 게임 판의 크기 N (4 ≤ N ≤ 100)이 주어진다. 그다음 N개 줄에는 각 칸에 적혀 있는 수가 N개씩 주어진다. 칸에 적혀있는 수는 0보다 크거나 같고, 9보다 작거나 같은 정수이며, 가장 오른쪽 아래 칸에는 항상 0이 주어진다.
출력
가장 왼쪽 위 칸에서 가장 오른쪽 아래 칸으로 문제의 규칙에 맞게 갈 수 있는 경로의 개수를 출력한다. 경로의 개수는 263-1보다 작거나 같다.
문제해결
dfs, bfs, dp로 해결 가능하다
약간 2차원 배열을 탐색한다는 사고(?)는 비슷한 것 같지만 이전 값들을 재활용한다는 점에서 DP로 분류할 수 있을 것 같다.
기본 뼈대는 평소 탐색 문제를 풀듯이 구성을 하였다.
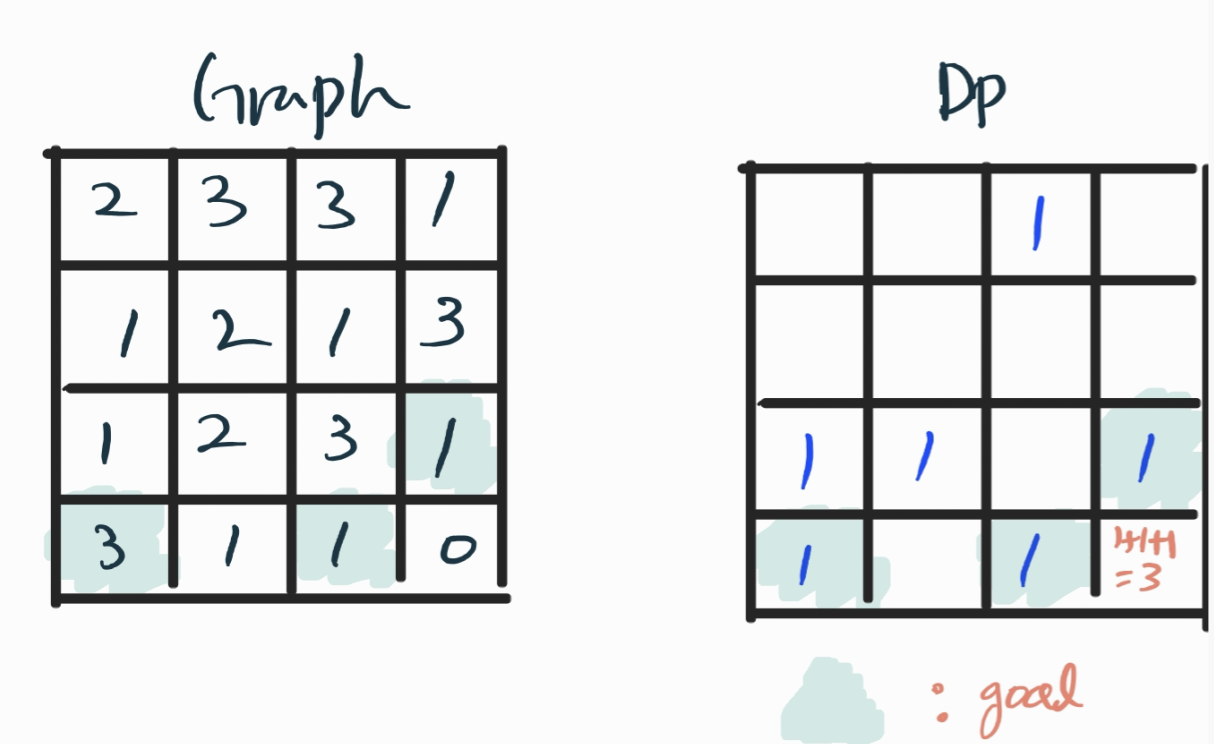
1. 첫 번째. dp배열을 정의하면 dp [i][j]는 방법의 수이다. (0,0) 시작점에서 시작해서 (n-1, n-1)까지 도달하면 1을 추가하는 식이다
dp(nx, ny)에 더하는 값에 대해 조금 혼동스러울 수 있는데 이전 값인 dp(i, j)를 0을 시작으로 계속 더해주어
dp(n-1, n-1)에는 '경로의 수'를 구할 수 있도록 해준다.
2. 두 번째. dp배열을 정의했으면 dp의 초기 설정을 해주어야 한다. dp의 경로의 수를 구하는 것이기에 dp [0][0] = 1 로시 작하여도
되지만 조금 더 정확하게 하기 위해 첫 도달점을 1로 초기화하였다.
3. 세 번째 점화식을 구한다. 1,2를 바탕으로 점화식을 구하면 된다. 'dp의 다음 값에 이전 값을 더해준다'를 식으로 풀면 아래와 같다.
오른쪽으로 이동할 땐 dp[nx][ny] = dp [i+graph[i][j]][j]
아래로 이동할 땐 dp[nx][ny] = dp[i][j+graph [i][j]] 로 나타낼 수 있고
아래 코드에는 nx, ny를 graph[i][j]만큼 이동하는 코드를 for문을 통해 나타냈다.
n = int(input())
graph = [list(map(int,input().split())) for _ in range(n)]
dp = [[0]*n for _ in range(n)]
dx,dy = [0,1],[1,0]
k = graph[0][0]
dp[k][0],dp[0][k] = 1,1
#dp[0][0]= 1##초기값설정
for i in range(n):
for j in range(n):
for t in range(2):
f = graph[i][j]
nx,ny = dx[t]*f + i , dy[t]*f + j
if i==n-1 and j==n-1:
continue
elif 0 <= nx < n and 0 <= ny < n:
dp[nx][ny] += dp[i][j]
print(dp[n-1][n-1])
'자료구조 알고리즘 > 백준' 카테고리의 다른 글
| [백준_python] 1937 : 욕심쟁이판다 (0) | 2022.05.05 |
|---|---|
| [백준_python] 1758_알바생강호 (0) | 2022.05.03 |
| [백준 9655] 돌게임_python (0) | 2022.05.01 |
| [백준_1010] 다리놓기_python (0) | 2022.05.01 |
| [백준_1439] 뒤집기_python (0) | 2022.04.28 |





댓글 영역