고정 헤더 영역
상세 컨텐츠
본문
https://www.acmicpc.net/problem/1010
1010번: 다리 놓기
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
www.acmicpc.net
문제
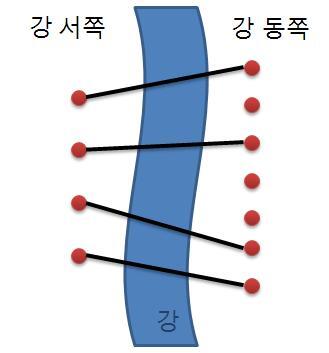
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)
재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.
입력
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그다음 줄부터 각각의 테스트 케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
출력
각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.
문제해결
1. 조합론으로 조합의 경우의 수를 구하는 방법
2. DP로 점화식을 세워 푸는 방법
1의 방법은 factorial함수를 구현해 n! // (n-r)! * r!로 mCn으로 푸는 방법이 있고
2는 0에서 30까지 주어지는 n, m의 값을 dp배열에 초기화하여 문제를 해결하는 방법이다.
1의 방법은 factorial함수만 구현하면 되는 거라 코드만 첨부하고 2에 대해 설명하겠다.
dp문제를 접할 땐 자잘 자잘한 것들로부터 큰 것을 구한다는 생각을 갖고
dp [m][n]의 값은 nCm으로 정의를 한 후 nC1의 값은 n으로 초기값을 지정해준다.
여기에서 규칙(?)을 한번 더 살펴보면 이전의 값들로부터 현재의 값을 구할 수 있단 생각이 들것이다.
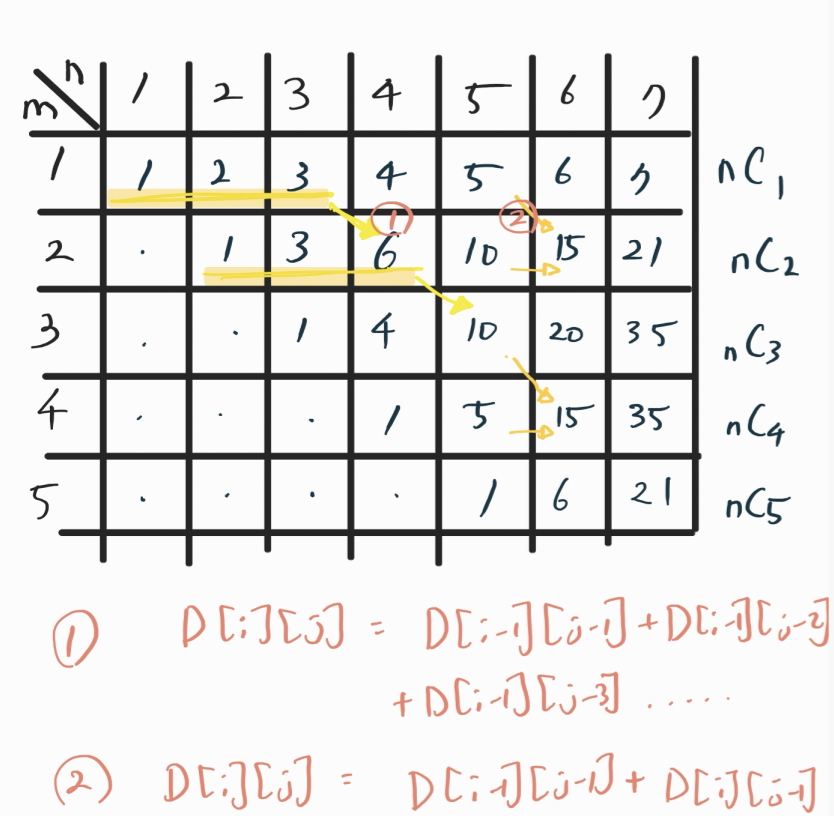
현재 값이 (i, j)라면 (0,0)부터 (i-1, j-1) 값까지의 합이 곧 (i, j)의 값임을 알 수가 있고 조금 더 나아가면
(i-1, j-1) 값과 (i, j-1) 합한 값이 (i, j) 임을 알 수 있다.
조금 더 이해를 쉽게 하기 위해 그림을 첨부하겠습니다.
요즘 DP능력을 기르기 위해 DP와 그리디 쪽만 문제를 풀고 있지만 현재의 나로선 1 의방 법이 훨씬 직관적이었다.
2의 방법을 떠올리기가 너무 힘들었다. DP가 직관적으로 와닿을 만큼 많은 문제를 풀고 접해봐야겠다.
#팩토리얼을 구현한 첫번째 방법
def f(x):
k = 0
res = 1
while x >k:
res *= x-k
k += 1
return res
n = int(input())
for _ in range(n):
a,b = map(int,input().split())
print(f(b)//(f(b-a)*f(a)))# dp를 활용한 두번째 방법
n = int(input())
dp = [[0]*31 for _ in range(31)]
for i in range(31):
dp[1][i] = i
for i in range(2,31):
for j in range(i,31):
dp[i][j] = dp[i-1][j-1]+dp[i][j-1]
for _ in range(n):
a,b = map(int,input().split())
print(dp[a][b])
'자료구조 알고리즘 > 백준' 카테고리의 다른 글
| [백준_python] 1890_점프 (0) | 2022.05.03 |
|---|---|
| [백준 9655] 돌게임_python (0) | 2022.05.01 |
| [백준_1439] 뒤집기_python (0) | 2022.04.28 |
| [백준_2217] 로프_python (0) | 2022.04.27 |
| [백준_1912]_연속합_python (0) | 2022.04.25 |





댓글 영역