고정 헤더 영역
상세 컨텐츠
본문
https://www.acmicpc.net/problem/1991
1991번: 트리 순회
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파
www.acmicpc.net
문제
이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.
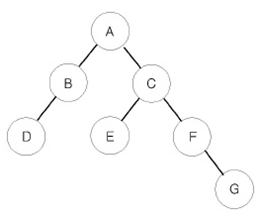
예를 들어 위와 같은 이진 트리가 입력되면,
- 전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
- 중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
- 후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)
가 된다.
입력
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파벳 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현한다.
출력
첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.
문제해결
전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)의 개념을 이해할 수 있는 트리순회 문제이다. 우선 위의 개념을 먼저 짚고 문제풀이를 하겠다
- 전위 순회(preorder traversal)란 우리가 기본적으로 알고있는 Depth First Search(DFS)방식과 유사하다고 보면된다. 깊이(뿌리)를 먼저 방문하는걸 우선순위로 둔다. 뿌리 노드 -> 왼쪽 자식 -> 오른쪽 자식 순이다
- 중위 순회(inorder traversal)는 왼쪽 하위 트리를 방문 후에 뿌리를 방문하는 것으로 조금 더 쉽게 설명하자면 트리를 정면에서 보았을 때, 깊이에 상관없이 왼쪽에서 오른쪽으로 먼저 보이는 노드순으로 방문하는 것을 말한다. 왼쪽 자식 -> 뿌리 -> 오른쪽 자식 순서로 이해하면 쉽다.
- 후위 순회(postorder traversal)는 하위노드를 방문후 그 부모격인 뿌리노드를 방문하는 것이다. 왼쪽 자식노드 -> 오른쪽 자식 노드 -> 뿌리 순서로 이해하면 된다.
이러한 개념을 바탕으로 문제를 보면 두번째줄부터 입력되는 값들을 부모노드와 자식노드(left, right)로 구분해주고
tree 라는 딕셔너리에 값들을 넣어주었다. key값이 중복되는 일이 없기에 리스트가아닌 딕셔너리를 사용하였다.
자식노드가 없는칸은 '.'으로 들어오기때문에 return으로 에외처리를 해주었다.
출력은 각 함수마다 재귀로 표현하였고 하나의 정수형이 출력으로 나오기 때문에 for문으로 이어붙이는 방법보다
print(x,end='')이 간결하여 출력부분의 공백만 신경써주어 출력하였다.
n = int(input())
tree = {}
for _ in range(n):
node , left, right = list(input().split())
tree[node] = left, right
def preorder(x):
if x =='.':
return
print(x,end='')
preorder(tree[x][0])
preorder(tree[x][1])
def inorder(x):
if x == '.':
return
inorder(tree[x][0])
print(x,end='')
inorder(tree[x][1])
def postorder(x):
if x == '.':
return
postorder(tree[x][0])
postorder(tree[x][1])
print(x,end='')
preorder('A')
print()
inorder('A')
print()
postorder('A')
'자료구조 알고리즘 > 백준' 카테고리의 다른 글
| [백준_2980] 도로와 신호등_python (0) | 2022.03.29 |
|---|---|
| [백준_14719] 빗물_python (0) | 2022.03.28 |
| [백준_2503] 숫자야구_Py (0) | 2022.03.23 |
| [백준_14500] 테트리미노_python (0) | 2022.03.22 |
| [백준_15663]N과M(9) (0) | 2022.03.21 |





댓글 영역